Spoiler: Click here to get the tl;dr advice

There’s almost never a good reason to give students a mass of 1 kilogram, and doing so can reinforce misconceptions about forces and units.

If you teach high school or introductory college physics (or just know the subject well), I wonder if you can tell what I’ve done wrong here:

a mass hanging from to strings at arbitrary angles, with tension protractors reading out the tension in the strings and their angles from horizontal

OK, well, I haven’t given you a lot of context.

Early in our study of forces, I make sure students see a lot of examples of objects that are not accelerating and the forces on them balance out, and conversely, a lot of examples of objects that are accelerating and the forces on them do not balance out. Sometimes we don’t even have to quantify the forces, we just have to know that some are bigger than others. Here are some examples that students see:

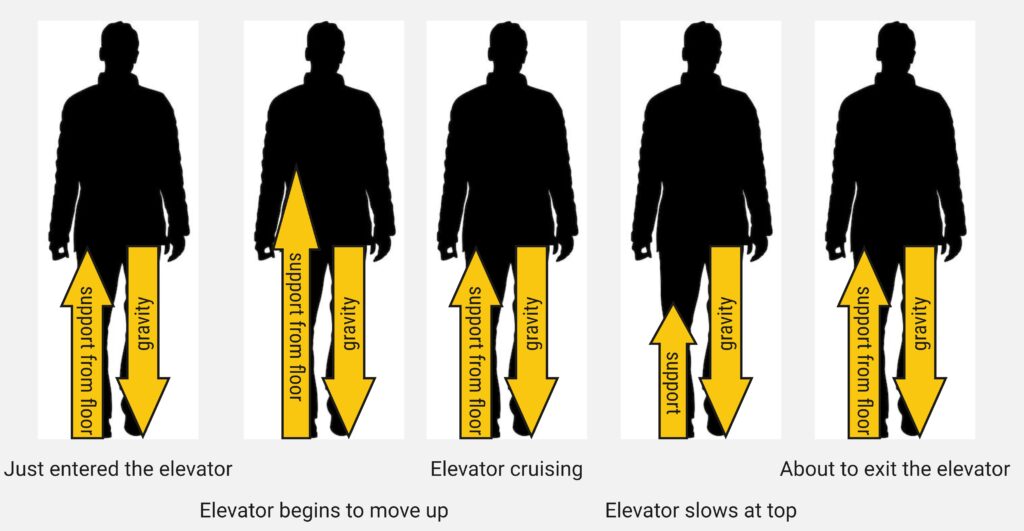
A person rides an elevator from the ground floor to the top floor.

a diagram showing the relative balance/imbalance of forces on a person during an elevator ride
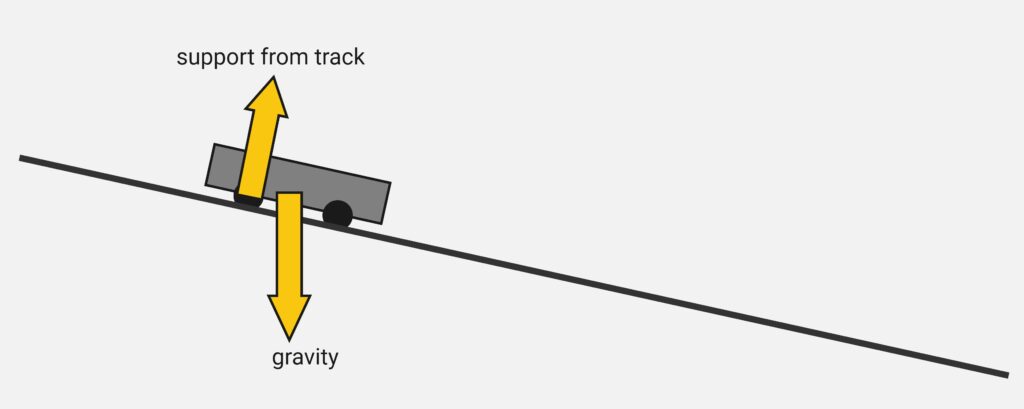
force diagram for a frictionless object sliding down an incline

An effectively frictionless car is released on an inclined track.

In the distant past, I noticed that some students left these exercises with an insidious misconception: From the kinds of examples we often look at, it’s easy to think that there’s always an up force to go with a down force, a left to go with a right, etc. And if there are any funny angles, then there’s always acceleration (because that left-right-up-down balance is upset).

So I make sure to emphasize the one in the photograph above, specifically because it involves an odd number of forces at “funny angles” that still balance out to zero acceleration.

Here it is again, but with the force vector information:

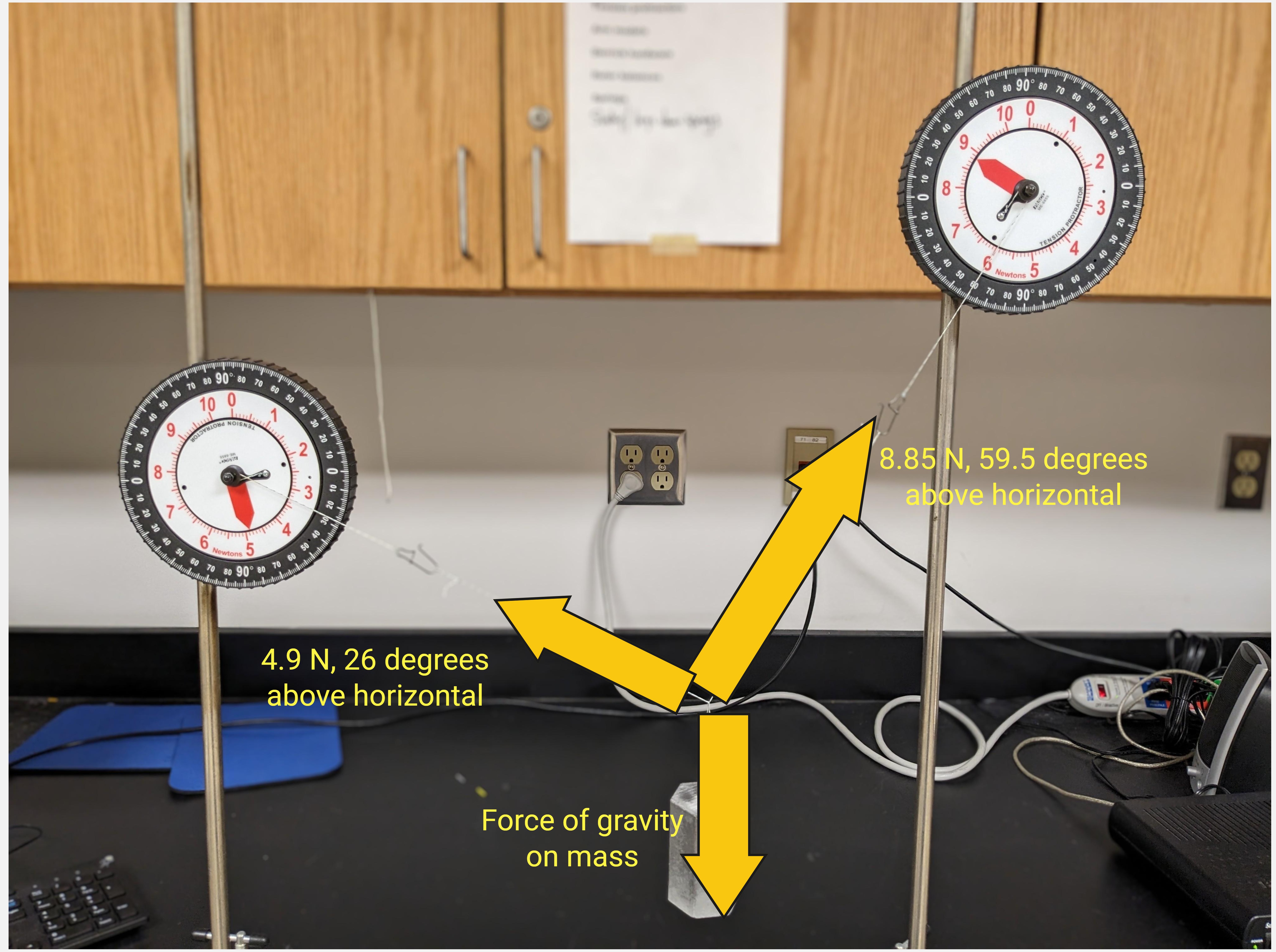
A mass hanging from angled strings. One string has 4.9N of tension pulling up and left at 26 degrees above horizontal; the other has 8.85N of tension pulling up and right at 59.5 degrees above horizontal.

Now can you see (or calculate) what I’ve done wrong?

This course does not require that a student have taken high school physics. But of course, some have. And somewhere students learn this sing-songy mantra:

“Gravity’s always nine point eight.”

When students drill a bunch of projectile motion kinematics problems, they learn (correctly) that the acceleration of gravity here at the surface of Earth is 9.8 m/s2, downward. But the precision of that statement is lost and it gets filed away as “gravity’s always 9.8” (there are never any units in this mantra [and that’s part of the problem]).

This (more-or-less correct) idea that the acceleration of gravity is always the same number transfers to an incorrect idea that the force of gravity is the same on every object. And what is that force of gravity? “Nine point eight,” of course! So on the above diagram, where I’ve labeled “force of gravity on mass,” many students have “9.8” written on their drawing. What they should have is Fgrav = mg, where m is the mass of the object in kg, and g = 9.8 N/kg, the strength of the gravitational field here at the surface of the Earth.

So what mistake did I make? Never give students a 1 kilogram mass, because it inadvertently reinforces the misconception that the force of gravity is always 9.8 Newtons.

I have had this realization before, but I’m forgetful, and dumb. Learn from my mistake!